문제링크:
https://www.acmicpc.net/problem/16639
길이가 N인 수식이 있다. 수식은 0보다 크거나 같고, 9보다 작거나 같은 정수와 연산자(+, -, ×)로 이루어져 있다. 곱하기의 연산자 우선순위가 더하기와 빼기보다 높기 때문에, 곱하기를 먼저 계산 해야 한다. 수식을 계산할 때는 왼쪽에서부터 순서대로 계산해야 한다. 예를 들어, 3+8×7-9×2의 결과는 41이다.
수식에 괄호를 추가하면, 괄호 안에 들어있는 식은 먼저 계산해야 한다. 예를 들어, 3+8×7-9×2에 괄호를 (3+8)×7-(9×2)와 같이 추가했으면, 식의 결과는 59가 된다. 중첩된 괄호도 사용할 수 있고, 괄호 안에 여러 개의 연산자가 들어 있어도 된다. 즉, 3+((8×7)-9)×2, 3+((8×7)-(9×2)), (3+8)×(7-9×2) 모두 올바른 식이고, 결과는 97, 41, -121이다.
수식이 주어졌을 때, 괄호를 적절히 추가해 만들 수 있는 식의 결과의 최댓값을 구하는 프로그램을 작성하시오. 추가하는 괄호 개수의 제한은 없으며, 추가하지 않아도 된다.

문제 정리
- 0~9, +-*
- 괄호는 중첩될 수 있다
- 괄호를 추가해서 만들 수 있는 최대값을 구해라
처음에는 완전탐색을 생각했는데, 괄호가 중첩되면 경우의 수가 너무 많아서 이 글을 참고해 Divide-and-conque + dp 로 풀었다.
사실 괄호 때문에 기존의 연산 우선순위는 효과가 없고 어떻게 괄호를 조합하냐에 초점을 맞춰야한다.
전체 식을 각 중심마다 left, right 둘로 계속 나눈다. (더 이상 나눠지지 않을 때까지)
제일 짧은 식부터 left값과 right값을 연산 중 최대값을 기록해 전체식의 최대값을 구한다.
주의할 점
식의 최대값을 구할 때 양수*양수 뿐만 아니라 음수*음수와 같은 경우도 양수가 되며 최대값이 될 수 있기 떄문에
식의 최대값은 maxdp에 최소값은 mindp에 저장한다.
식을 left, right 둘로 나눴을 때 계산값은 4가지다
- left max * right max
- left max * right min
- left min * right max
- left min * right min
구할 수 있는 값 중 최대, 최소값을 각각 maxdp, mindp에 저장하고
dp[i][j] 의 최대값은 max[i][j], 최소값은 mindp[i][j] 이다.
이런식으로 저장한 뒤 마지막 maxdp[0][마지막 인덱스]를 리턴한다.
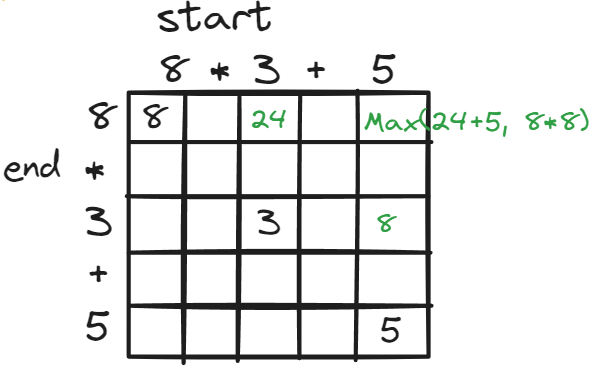
예를 들어 8*3+5라는 식을 둘로 나누면 8, (3+5) 혹은 (8*3), 5 로 나눌 수 있다.
maxdp[0][2] 는 0~2 left의 최대값 즉 8*3 = 24 (mindp[0][2]도 동일하다)
maxdp[2][4] 는 2~4 right의 최대값 3+5 = 8 (mindp[2][4]도 동일하다)
dp[0][4] 는 0~4 전체 식의 최대값이다
// 입력 처리
const file = "/dev/stdin";
// const file = "test.txt";
let input = require("fs").readFileSync(file).toString().trim().split("\n");
const N = parseInt(input[0]);
const equation = input[1];
// 초기화 dp[i][i] = i
let maxdp = Array.from({ length: N }, () =>
Array.from({ length: N }, () => -Infinity)
);
let mindp = Array.from({ length: N }, () =>
Array.from({ length: N }, () => Infinity)
);
for (let i = 0; i < N; i++) {
if (!isNaN(parseInt(equation[i]))) {
maxdp[i][i] = parseInt(equation[i]);
mindp[i][i] = parseInt(equation[i]);
}
}
// top to bottom
dp(0, N - 1);
console.log(maxdp[0][N - 1]);
// i에서 j까지 [최소, 최대] 리턴
function dp(i, j) {
if (i === j) return [parseInt(equation[i]), parseInt(equation[i])];
if (maxdp[i][j] !== -Infinity && mindp[i][j] !== Infinity) {
return [mindp[i][j], maxdp[i][j]];
}
for (let mid = i + 1; mid < j; mid += 2) {
let ops = equation[mid];
let [leftMin, leftMax] = dp(i, mid - 1);
let [rightMin, rightMax] = dp(mid + 1, j);
const calRes = [];
calRes.push(calc(leftMax, rightMax, ops));
calRes.push(calc(leftMax, rightMin, ops));
calRes.push(calc(leftMin, rightMax, ops));
calRes.push(calc(leftMin, rightMin, ops));
calRes.sort((a, b) => a - b);
maxdp[i][j] = Math.max(maxdp[i][j], calRes[3]);
mindp[i][j] = Math.min(mindp[i][j], calRes[0]);
}
return [mindp[i][j], maxdp[i][j]];
}
function calc(a, b, op) {
switch (op) {
case "+":
return a + b;
case "-":
return a - b;
case "*":
return a * b;
}
}

'알고리즘' 카테고리의 다른 글
| [백준] 2493번 탑 JS 풀이 (0) | 2024.04.25 |
|---|---|
| [백준] 쇠막대기 (0) | 2024.03.14 |
| [프로그래머스] 가장 긴 팰린드롬 (0) | 2024.02.22 |
| [프로그래머스] 단속 카메라 (0) | 2024.02.21 |
| [프로그래머스] 택배 배달과 수거하기 (0) | 2024.02.14 |


