https://school.programmers.co.kr/learn/courses/30/lessons/12936

첫번째 풀이 (시간초과)
모든 경우를 구한 뒤 k번째 결과를 리턴했다.
// 백트래킹 순열
function solution(n, k) {
var answer = [];
const arr = Array.from({length: n}, (_, i) => i+1);
function bt(acc, remain) {
if (!remain.length) {
answer.push(acc);
return;
}
for (const r of remain) {
bt([...acc, r], remain.filter(e => e !== r));
}
}
bt([], arr);
return answer[k-1];
}
가장 큰 자연수가 20이므로 시간 복잡도가 초과한다.
20! = 2432902008176640000

두번째 풀이 (성공)
첫번째 풀이처럼 모든 경우를 구한 뒤 k번째를 구하려고 하면 n이 커질수록 시간초과한다.
=> 모든 경우를 구하지말고 팩토리얼로 각 자릿수마다 가능한 경우의 수를 구하고, 전체 갯수k를 각 범위당 경우의 갯수로 나누며 k번째 경우를 구해야한다.

쉽게 얘기하자면 예를 들어 사람이 [1,2,3]이고 5번째 경우를 구할 때
1번째 경우인 [1,2,3] 부터 전부 구하는게 아니라 각 자릿 수마다 가능한 경우의 수를 계산해 숫자의 조합을 만드는 것이다.
첫번째 자리가 정해진 경우, 예를 들어 [1, _, _ ] 일때는 [1, 2, 3], [1, 3, 2] 로 2*1 = 2가지 경우가 있다.
우리가 원하는 건 5번째의 경우인데 한 그룹당 2! 가지의 경우가 있으므로 계산해보면
5 / 2! = 몫2 나머지 1로, 5번째 경우는 3번째 그룹의 1번째 경우라는 것을 알 수 있다. 이를 밑의 공식으로 정리할 수 있다.

factorial(n-1) = n번째 수가 정해지고 n-1로 만들수 있는 모든 경우
selectedIndex = 앞의 수 부터 선택한 인덱스 = k번째 수가 속한 그룹
하지만 한 가지 주의할 점이 있다. 만약 나머지가 0으로 나눠떨어지면 몇 번째 그룹인지 계산하는 방법이 살짝 다르다.
예를 들어 4번째 경우는 4 / 2! = 몫2 나머지 0으로, 이는 3번째 그룹이 아닌 2번째 그룹의 마지막 경우이다.
따라서 만약 나머지가 0이면 selectedIndex를 -1 해줘야한다.
그럼 이제 본격적으로 알고리즘을 구현해보자
우선 계산할때마다 팩토리얼을 구하는건 비효율적이므로 먼저 dp로 팩토리얼을 구한다.
팩토리얼이란
양의 정수 n에 대해 1부터 n까지의 모든 양의 정수를 곱한 값이다
factorial( i ) = factorial( i - 1) * i
0! 와 1! 는 1이다
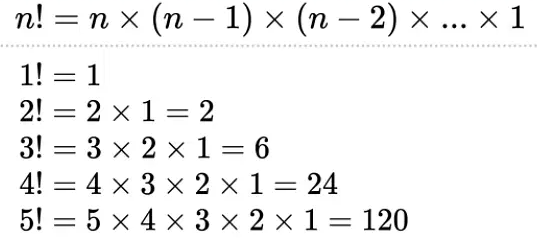
- 팩토리얼을 구한 뒤, 백트래킹으로 남은 사람이 없을 때까지 즉 n이 0이 될때까지 k번째 경우를 찾는다.
- 매 선택마다 선택된 인덱스인 사람의 값인 arr[selectedIndex]는 acc에 넣어주고 해당 인덱스는 arr에서 제거한다.
- 남은 경우 수인 k는 기존의 k를 팩토리얼(n-1)의 크기로 나눈 나머지로 갱신한다.
// 백트래킹 순열
function solution(n, k) {
var answer = [];
let arr = Array.from({ length: n }, (_, i) => i + 1);
const factorialArr = [1, 1];
function getFactorialArr(n) {
for (let i = 2; i <= n; ++i) {
factorialArr[i] = i * factorialArr[i - 1];
}
}
getFactorialArr(n);
function bt(n, k, acc) {
if (n === 0) {
answer = acc.concat(arr);
return;
}
let selectedIndex = Math.floor(k / factorialArr[n - 1]);
k = k % factorialArr[n - 1];
if (k === 0) {
selectedIndex--;
}
bt(n - 1, k, [...acc, ...arr.splice(selectedIndex, 1)]);
}
bt(n, k, []);
return answer;
}

처음엔 봤을때 쉬워보였지만 핵심개념을 수립하고 코드를 짜면서 인덱스와 숫자 하나 차이로 헷갈렸던 문제다.
새로운 방식으로 경우를 구하는게 흥미로웠다.
'알고리즘' 카테고리의 다른 글
| H-Index (0) | 2023.12.08 |
|---|---|
| [프로그래머스 lv2] 숫자 카드 나누기 (0) | 2023.12.08 |
| 롤케이크 자르기 (0) | 2023.12.07 |
| [프로그래머스 LV2] 마법의 엘리베이터 JS (0) | 2023.12.07 |
| 비트마스킹 (0) | 2023.12.06 |



